Hi Prof. Peixoto,
I was testing the OverlapBlockState model on a synthetic graph.
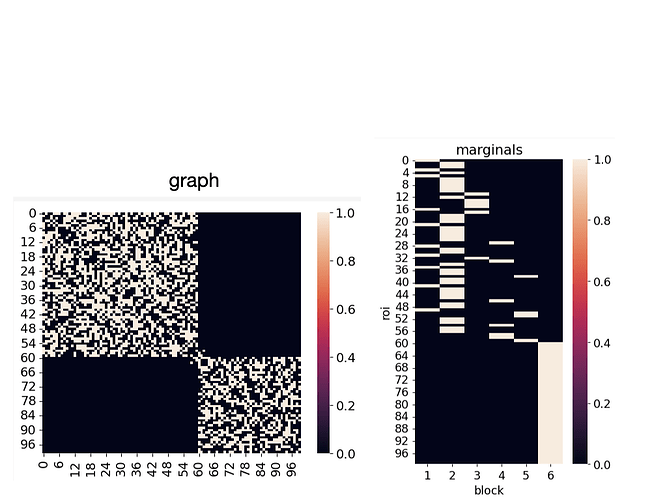
The graph consists of two assortative blocks that are minimally connected to each other.
I was expecting the SBM to infer two blocks that overlap at those minimal nodes, but it infers many blocks.
This is non-degree-corrected SBM(degree-corrected model takes forever to converge, so couldn’t run that).
Am I missing something in my understanding?
Attached are the grapn and marginal distributions of nodes (roi means region of interest, a.k.a node):
Also, it looks like SBM breaks the bigger block into many and keeps the smaller block intact.
The following is the accompanying code.
import numpy as np
import graph_tool.all as gt
# plotting
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
# ignore user warnings
import warnings
warnings.filterwarnings("ignore") #, category=UserWarning)
class ARGS():
pass
args = ARGS()
args.SEED = 100
args.num_repeats = 100
gt.seed_rng(args.SEED)
np.random.seed(args.SEED)
args.num_rois = 100
def add_block(A, pos, size, density):
# create block of given density
nrows, ncols = size
a = (np.random.rand(nrows,ncols)<density).astype('int')
i, j = pos
A[i : i+nrows, j:j+ncols] = a
return A
def normalize_A(A):
A = (A + A.T) / 2
A -= np.diag(np.diag(A))
return (A>0).astype('int')
def make_graph_from_A(G):
G = np.tril(G)
edges = np.where(G)
edge_list = list(zip(*(*edges, G[edges])))
g = gt.Graph(
edge_list,
eprops=[('weight', 'double')],
directed=False
)
return g
A = np.zeros((args.num_rois, args.num_rois))
A = add_block(A, (0,0), (60, 60), 0.3)
A = add_block(A, (60, 60), (40, 40), 0.3)
A = add_block(A, (57, 57), (6, 6), 0.3)
A = normalize_A(A)
sns.heatmap(A)
g = make_graph_from_A(A)
def mcmc_eq(args, state):
bs = [] # partitions
Bs = np.zeros(g.num_vertices() + 1) # number of partitions
mdls = [] # entropies
def collect_partitions(s):
bs.append(s.b.a.copy())
B = s.get_nonempty_B()
Bs[B] += 1
mdls.append(s.entropy())
gt.mcmc_equilibrate(
state,
wait=args.wait,
mcmc_args=dict(niter=args.niter),
callback=collect_partitions,
)
return state, bs, Bs, mdls
def get_partition_mode(args, g, state, bs, Bs):
pmode = gt.PartitionModeState(bs, converge=True)
return pmode
def rescale(X):
X /= np.expand_dims(np.sum(X, axis=-1), axis=-1)
X = np.nan_to_num(X)
X = np.round(X, decimals=3)
return X
def get_marginals(args, g, state, mode):
# vertex marginals of the graph in the state,
# if overlapping state, it is graph of half-edges
sg = state.g
B = mode.get_B()
print(B)
v_marginals = np.zeros((sg.num_vertices(), B))
for idx, prob in zip(sg.iter_vertices(), mode.get_marginal(sg)):
prob = list(prob)
prob = prob if len(prob) < B else prob[:B]
prob = prob + [0]*(B - len(prob))
v_marginals[idx] = np.array(prob)
v_marginals = rescale(v_marginals)
if not state.overlap:
marginals = v_marginals.copy()
else:
# average of probs. of half-edges incident on a vertex
marginals = np.zeros((g.num_vertices(), v_marginals.shape[-1]))
for v, hes in zip(g.iter_vertices(), state.half_edges):
marginals[v] = np.mean(v_marginals[hes], axis=0)
return marginals
def fit_sbm(args, g, state=gt.BlockState, state_args=dict()):
state = gt.minimize_blockmodel_dl(g, state=state, state_args=state_args)
state, bs, Bs, mdls = mcmc_eq(args, state)
pmode = get_partition_mode(args, g, state, bs, Bs)
marginal = get_marginals(args, g, state, pmode)
return marginal, pmode, state, bs, Bs, mdls
args.wait = 1000
args.niter = 10
marginal, pmode, state, bs, Bs, mdls = fit_sbm(args, g, gt.OverlapBlockState, state_args=dict(deg_corr=False))
ncols = 1
nrows = 1
fig, axs = plt.subplots(
nrows=nrows, ncols=ncols,
figsize=(4*ncols, 6*nrows), dpi=90,
sharex=True, sharey=True
)
fig.tight_layout()
ax = axs
sns.heatmap(marginal, ax=ax,)# annot=True, fmt='.2f')
ax.set(
title=f'marginals',
xlabel='block', ylabel='roi',
xticklabels=np.arange(marginal.shape[-1])+1,
)
Thank you,
Govinda