I am very new to graph tool and graphs in general and hence this naive question.
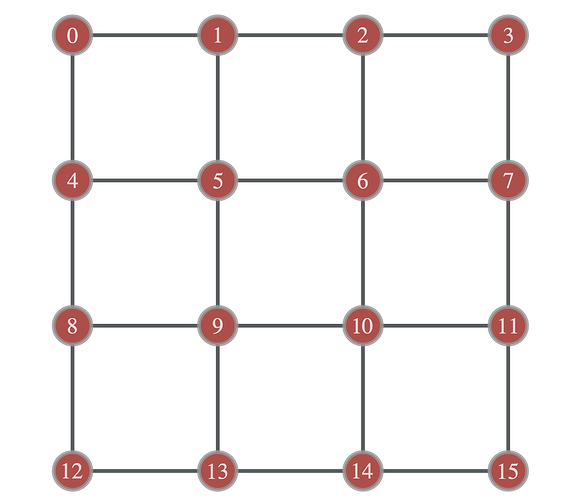
I have created a 2D square lattice graph as such:
L=4
g = gt.lattice([L,L])
idx = g.vertex_index.copy()
x = g.new_vertex_property("double")
y = g.new_vertex_property("double")
x.a = idx.a % L
y.a = idx.a // L
pos = group_vector_property([x,y])
graph_draw(g,pos,vertex_text=g.vertex_index)
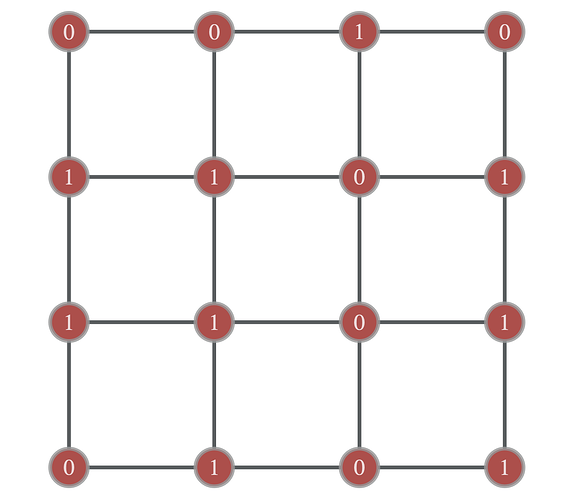
And then I add a property called ‘act_stat’ to each vertex:
(act_stat can be 0 or 1):
act_stat = g.new_vertex_property("int")
act_stat.a = np.random.randint(2,size=L**2)
graph_draw(g,pos,vertex_text=act_stat)
How do I randomly find a vertex which has an ‘act_stat = 0’, and find all the vertices with ‘act_stat=0’ connected to it either directly or through a line of ‘act_stat=1’ vertices.
I do not want to delete the ‘act_stat=1’ vertices using filtering because the goal is to find the path of minimum distances between the randomly chosen ‘act_stat=0’ and all other ‘act_stat=0’ vertices connected to it either directly or through a line of ‘act_stat=1’ vertices.
Any tips on which functions to use will also be greatly appreciated.
From what I understand, I need to use Djikstra’s search algorithm to find the shortest paths between a randomly choses source ‘act_stat=0’ vertex and all other ‘act_stat=0’ vertices connected to it directly or via ‘act_stat=1’.
But how do I find all the ‘act_stat=0’ vertices connected to the source ‘act_stat=0’ vertex? Should I first run some kind of depth-first search to find a list of all ‘act_stat=0’ vertices and then for each vertex in that list, run a Djikstra search to find the path of minimum distance to that vertex?