Hi Tiago,
I was recently comparing the behavior of the clustering coefficient in
different graph libraries and I was surprised by the results given by
graph-tool with parallel edges:
import graph_tool as gt
from graph_tool.clustering import local_clustering
from graph_tool.stats import remove_parallel_edges
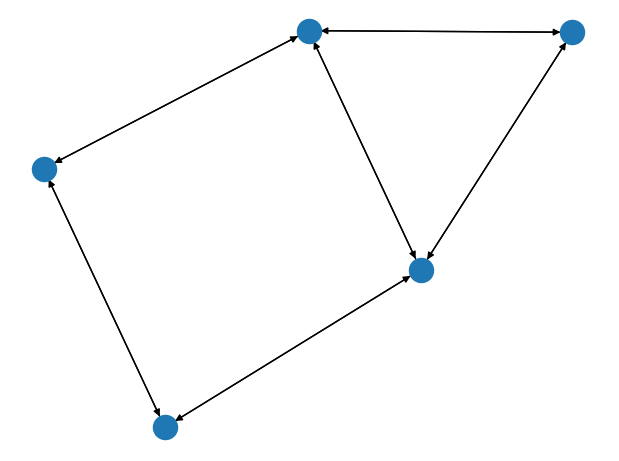
num_nodes = 5
edge_list = [(0, 3), (3, 0), (1, 0), (0, 1), (1, 2), (2, 1), (2, 4),
(4, 2), (4, 1), (1, 4), (4, 3), (3, 4)]
g = gt.Graph()
g.add_vertex(num_nodes)
g.add_edge_list(edge_list)
print(local_clustering(g, undirected=False).a)
print(local_clustering(g, undirected=True).a)
g.set_directed(False)
remove_parallel_edges(g)
print(local_clustering(g, undirected=True).a)
Gives:
[0. 0.33333333 1. 0. 0.33333333]
[0. 0.26666667 0.66666667 0. 0.26666667]
[0. 0.33333333 1. 0. 0.33333333]
And I must say I was expecting the same result for all three ^^
The graph:
From what I understand, then, it seems that, when using
undirected=True, graph-tool considers reciprocal edges as two different
ones and considers the possible triangles between parallel edges as
distinct.
Is this desired behavior, and if so, why?
I know it stems from the mathematical formula, but I think this one was
derived from simple graphs and I'm not sure I see the physical meaning
of the "extension" to parallel edges, besides the fact that it would
perhaps give the same result as weighting the edges by their number.
If this is indeed desired, is there a quick way to do the equivalent of
setting the graph to undirected and removing the parallel edges in
"view-mode" (i.e. making the removal temporary, like a filter)?
Thanks in advance for your help and for your work on graph-tool.
Best,
Tanguy
attachment.html (2.88 KB)